A Critique of Graham Hancock’s Forced Numerical Relationship between the Great Pyramid of Giza and Earth’s Dimensions – 1

Graham Hancock regularly draws attention to what he considers mystical relationships between the Great Pyramid of Giza and the radius, circumference, and axial precession of the earth (Figure 1, shown on page 6, illustrates axial precession). Proponents of these “mystical” relationships contend, in addition to existing in the first place, that the relationships must be purposeful and therefore provide direct evidence of advanced capabilities in technology, mathematics, and precise astronomical observing techniques that scholars have long asserted were not available to humans when the pyramids were constructed. Others may find these esoteric connections between the Great Pyramid and the earth to be dubious given many natural observations that explain the corpus of geometric semblances without ascribing a precise knowledge of π to its builders, or contending that the Great Pyramid was coded with some of earth’s key parameters that Hancock refers to as earth’s “cardinal dimensions.”

The explanations offered here extend inherently from simple and reasonable pyramidic design techniques, though the explanations themselves are sometimes technical. While each concept is basic, it can be convoluted to explain them in writing. It is quite easy for Hancock to concoct fascinating claims and appeal to unknown advanced intellects for justification, but cumbersome to demonstrate how his superficially profound relationships evaporate when relying on a range of actual measurements and observations. This is especially true when so many people prefer being amazed by mystical accounts over genuine assessments of human ingenuity.

In this 5-minute video, Hancock summarizes some of his fantastic claims (Hancock 2017).

Though Hancock is widely popular, he is not alone in publishing revelations of hidden codes and lost ancient secrets. He is part of a troupe of Western esotericists that has grown in popularity over the past 30 or so years. This contemporary esotericism, though likely rooted in Pyramidology and the Christian Identity Movement, appears generally more focused on a pseudoarchaeological message of ancient and lost scientific knowledge, while the meme that divine pyramidic codes link English heritage to Biblical racial identities, has lost favor for various reasons (Keach 2011).

Prominent mentors of this esoteric movement include Eckhart R. Schmitz, Edward J. Nightingale, Robert Bauval, Adrian Gilbert, Zecharia Sitchin and others. Schmitz and Nightingale particularly circulate various hidden numerical relationships that they both perceive or construct. This is seen in Schmitz’s book; The Great Pyramid of Giza: Decoding the Measure of a Monument, details of which are included on Hancock’s website (Schmitz 2012), and in Nightingale’s book, The Giza Temple, a summary of which Hancock again promotes on his website (Nightingale 2015).

This critique focuses on Hancock’s and others’ claims that the Great Pyramid’s proportions contain hidden codes, and that those codes demonstrate proof that the ancient builders were aware of earth’s precession and circumference and capable of calculating both to a degree of accuracy inconsistent with ancient knowledge and technology (Hancock 2016).

Basic geometry and mathematics are used to discuss π, Ø, precession, circumference, radii of the earth, etc., and to rebut claims of alien or ancient hyperadvanced human contributions to the design characteristics of the Great Pyramid. However, the practical logistics of how blocks were quarried, carved, moved, polished, and stacked is ignored since those aspects are regularly addressed and demonstrated by others (“Egyptian Pyramid Construction Techniques.” 2019). Instead, attention is focused on specific observations that indicate the intrinsic, trivial, or nonexistent relationships shared between the Great Pyramid of Giza and the earth.

Hancock Being Hancock

For those new to Hancock, here is an example of his penchant for hyperbole, esotericism, and general gravitation towards pseudoarchaeology. In this excerpt from the video link above, Hancock speaks to the alignment of the Great Pyramid:

The Great Pyramid is locked in to the cardinal dimensions of our planet. The Great Pyramid is targeted on true north, within three sixtieth of a single degree. Now, no modern builder would create a large building and add onto his or her shoulders the additional burden of aligning it to true north within a fraction of a single degree. They just wouldn’t get it; they wouldn’t understand why it was important to do that (Hancock 2017).

One doesn’t need to understand algebra, the earth’s geometry, or methods of astronomical observation to recognize Hancock’s desire to sensationalize and mysticize pyramidic construction techniques upon hearing that statement.

Firstly, monument builders, both modern and ancient, are fully capable of understanding why they might align public or private architecture to any specified azimuth or any specific placement, both from a purely functional perspective; i.e. building locations and orientations are typically specified, as well as a symbolic perspective; i.e. true north, due east, or “towards Mecca” all have natural interpretive understandings that might appeal to an architect or group of people. Symbolic affinities are especially appealing for monuments but can be manifested in any architectural undertaking.

Secondly, constructing a building’s location and alignment with great precision would be trivial given surveying technology and methods that exist today. Modern equipment measures the propagation of electromagnetic waves of varied wavelengths and can be as precise as 0.5 to 5 mm at distances of up to 3 km (“Electronic Distance Measurement Instrument” 2017).

Despite deep admiration for the construction techniques and precision of the ancient Egyptians, suggesting that builders today would struggle to reproduce such an alignment is either foolish or disingenuous. Drawing attention to the impressive accuracy achieved by the pyramid builders is certainly a legitimate way to recognize them for their ingenuity, religious like attention, and remarkable application of technologies available to bronze age monument builders. However, this recognition can be offered without suggesting that surveyors and builders today couldn’t recreate or surpass ancient accuracy and precision.

Geometry, Precision, and Purpose

From the video:

… to incorporate into its dimensions the dimensions of our planet. I don’t want to get too numerical or possibly even boring here, but if you take the height of the Great Pyramid and multiply it by 43,200, you get the polar radius of the earth. And if you measure the base perimeter of the Great Pyramid accurately, and multiply that measurement by 43,200, you get the equatorial circumference of the earth …

… and the scale is not random. The number 43,200 is derived from a key motion of the earth, which is called the precession of the earth’s axis. The earth wobbles on its axis very slowly at the rate of one degree every 72 years. And 43,200 is a multiple of 72. In fact, I think it is 600 times 72 (Hancock 2017).

In the above paragraph, Hancock emphasizes that the primary dimensions of the Great Pyramid directly equate to the earth. He marvels at these relationships as if to suggest that these relationships are so mystical they reveal knowledge of the builders that cannot be explained by the known technology of ancient Egypt alone. In other interviews and writings Hancock explicitly claims these relationships demonstrate the existence of unknown hyper-advanced Pleistocene civilizations (Hancock 2016).

Note that criticizing Hancock’s specific claims that the ancient Egyptians coded precession and earth’s dimensions into the Great Pyramid does not imply a strict denial that the ancient Egyptians understood precession and made some estimate of it, or that they built the Great Pyramid to some purposeful size they felt was harmonious to either the earth or nature. This critique is simply intended to show that Hancock’s support for these claims is entirely forced or imagined.

In the sections that follow, these four main ideas are demonstrated to rebut Hancock’s appeal to hyperadvanced civilizations:

1) Observed relationships between the dimensions of the Great Pyramid and the earth can be completely natural: Any pyramid constructed with the geometry of a simply circle in mind is naturally comparable and proportional to any circle or sphere. This is easy to show.

2) 43,200 does not indicate precession: The scalar 43,200 is not suggestive of a knowledge of precession and has no direct association with precession or any of earth’s other parameters.

3) 43,200 is probably not the Great Pyramid scalar if such a scalar relating the Great Pyramid to the earth even exists: Hancock (and others such as Eckhart) cherry pick their measurements from a wide range of possibilities, to demonstrate that the ratio of the Great Pyramid to the earth is precisely 1:43,200. Even if the ancient Egyptians intended for the Great Pyramid to be scaled to any dimension or natural movement of the earth, there is no evidence that the scale is precisely 1:43,200.

4) Alternative (including more precise) values for precession and the size of the earth can’t be demonstrated: After refuting Hancock et al. claims that the ancient Egyptians incorporated the value of 25,920 years precession (25,920 is a fairly precise value of precession and, if understood, would indicate impressive technology for ancient astronomers), the earth’s equatorial circumference, and the earth’s polar radius into the Great Pyramid’s dimensions, it is demonstrated that it is also impossible to prove that even more accurate and precise values were coded into the Great Pyramid. This added effort is offered since a reader might consider that Hancock et al. are correct to recognize that the ancient Egyptians coded both precession and earth’s dimensions into the Great Pyramid, but their error is that they failed to realize that the Great Pyramid coded greater precision than Hancock recognizes. The extended analysis is presented in Appendix E.

Evaluating the Relationship between the Great Pyramid, Earth’s Polar Radius, and Earth’s Equatorial Circumference

To begin with, Hancock claims that the height and base perimeter of the Great Pyramid equate to both the radius and circumference, respectively, of a circle when multiplied by the same constant, 43,200. The circle, in this case, is a cross section of the nearly spherical earth. The constant 43,200 will be investigated and discussed in later sections, but for now discussion will focus on why the height and perimeter of the Great Pyramid can be related to the earth when each are multiplied by some scalar constant.

If a pyramid is purposefully constructed to incorporate the geometry of a circle; that is, if its height is selected to be equivalent to the radius of a circle with a circumference equal to the pyramid’s base perimeter, or vice versa, if the base perimeter is selected based on the circumference of a circle with a radius equal to the pyramid’s height, then not only would π be naturally and systematically incorporated into that pyramid, but those core dimensions of the pyramid would naturally be proportional to any circle, including those of the earth. This is true whether the builder is aware of π or not or possesses a precise estimate of π or not.

AXIOM 1: Any pyramid built in congruence with the basic geometry of a circle will incidentally contain π and be proportional to all circles and spheres.

There are other interesting and novel explanations for “accidentally” incorporating π into the Great Pyramid’s construction including a method where the base is laid out using a wheel (Yochim 2017). Attention is drawn to the association with π because Hancock and his ilk like to claim that π was also coded within the pyramid in another mystical assertion that the real and transcendental number, π, was understood to many decimal places (Schmitz 2012). It is further shown in Appendix F that the transcendental number Ø (commonly referred to as the “golden ratio”) would also be intrinsically fixed into the geometry of the pyramid designed with a circle in mind.

If the Great Pyramid was built in such a manner it would be comparable to a circle of any size by simply multiplying the pyramid dimensions by a scalar. The circle Hancock selected for comparison is the one formed by the cross-section of the earth but about 43,200 times bigger than the Great Pyramid (Again, more about 43,200 in later sections). Hancock emphasizing his curiosity that the Great Pyramid somehow describes both the radius AND the circumference of the earth is trivial for any pyramid constructed with a circle in mind since the pyramid can be related to all circles. Of course, most cross sections of the earth are slightly different in size (and not perfect circles), but, as will be shown, the Great Pyramid’s dimensions still fail to align with any of earth’s dimensions when using a single scalar and reasonable measurements of the pyramid.

To illustrate how easy it is to associate the Great Pyramid with a circle, some simple algebra is used along with a very selective choice in the radius of the earth (a range of values are available) to show, in Appendix B, that the volume of the Great Pyramid can also be equated to the volume of the earth using the scalar 43,200 (though 43,200 is not a unique solution, the process can be accomplished for many scalars within a range of possibilities). If Hancock himself emphasized that 43,200 also described the volume of the earth, without explaining how naturally volume of a sphere can be linked to any structure that unintentionally incorporated π, or that effort is required when choosing each input parameter, it would appear to be yet another mystical relationship.

Explanations have been simplified up to this point by discussing one circle and one radius. But the earth has more than one radius, and Hancock specifies that the Great Pyramid’s height is specifically comparable to the polar radius and the perimeter is specifically comparable to the equatorial circumference. If that distinction made by Hancock was strictly correct, and the polar radius does equate solely and specifically to the pyramid’s height, and the equatorial circumference equates solely and specifically to the pyramid’s base perimeter, that would be of great interest. But those identities are not specifically satisfied by any of the various earth’s radii as explained further in Appendix A, and in the next section. To the contrary, it can be demonstrated that the height and base perimeter of the Great Pyramid more likely describe the same circle which would naturally be the case if the pyramid was designed with the geometry of any simple circle in mind.

Evaluating Hancock’s Calculations and the Number 43,200

Given the circumference of a circle, C = 2πr, a pyramid can be designed with that geometry in mind, but without understanding the precise value of π. As was explained in the section above, this can be done by setting the height, “h”, of the pyramid to be “r”, and the base perimeter to be “C”. Each side of the base of the pyramid is then C/4 or (2πh)/4.

• Equation 1: Circumference of a Circle = C = 2πr

• Eq. 2: Pyramid height = h

Setting a pyramid’s height equal to any circle’s radius gives: •

• Eq. 3: Pyramid height = h = r

• Eq. 4: Pyramid perimeter = 4 * Base side = 4*b

Setting a pyramid’s perimeter equal to any circle’s circumference gives:

• Eq. 5: Pyramid perimeter = 4*b = (2πh)

• Eq. 6: Pyramid side = Eq. 5 divided by 4 = (2πh)/4 = (πh)/2

One can then multiply “h” of any pyramid by “k” (a scalar) and directly relate the pyramid to a circle that is “k” times bigger. According to Hancock, to equate the Great Pyramid to the earth, k = 43,200. Hancock also claims, more specifically, that:

• Eq. 7: Great Pyramid height * k = the radius of the earth at the poles

• Eq. 8: Great Pyramid perimeter * k = the circumference of the earth at the equator

The earth is not a perfect sphere and therefore has multiple implied radii in addition to multiple actual radii. More is explained in Appendix A; but suffice to say that if one desires to satisfy Eq. 7 and Eq. 8 with a single scalar close to the number 43,000, one can proceed with some confidence because of the many radii choices available (in addition to choices in the underlying pyramid measurements themselves given the deteriorated state of the pyramid). Essentially, any radius from 6,357 km to 6,400 km can be selected as the polar radius. Likewise, the equatorial radius can range from 6,335 km to 6,378 km, resulting in an equatorial circumference range of 39,804 km to 40,074 km.

Continuing with Eq. 7 (with “k” = 43,200):

• Eq. 7: Great Pyramid height * 43,200 = Polar Radius

146.58 m * 43,200 = 6,332.26 km

Here the preferred value for the pyramid height, as it is assumed to have existed in antiquity, is chosen. It is now greatly deteriorated and smaller than its original size. Much more is discussed about the Great Pyramid size in Appendix E. However, using the assumed height results in a polar radius that is outside the range of possible polar radii. Conversely, if either of the two extreme values for the polar radius (N = 6,357 or R = 6,400) are chosen, pyramid heights of about 148.15 m and 147.18 m, respectively, are implied. These implied heights unfortunately fail to form a range around the assumed original height of 146.58 m.

The radius equating to the height of the pyramid and the constant 43,200 is 6,332.26 km and does not match any of the many radii given in Appendix A. The calculated value of 6,332.26 most closely matches the meridional radius of curvature, M, at about 0 degrees latitude (the equator). (FYI: The latitude of the Great Pyramid is 29.9792 degrees North).

Continuing now with Eq. 8:

• Eq. 8: Great Pyramid perimeter * 43,200 = Equatorial Circumference

230.34 m * 4 * 43,200 = 39,802.75 km (actual circumference is 40,075 km). And 39,802.75 km equates to an implied radius of 6,334.80 km.

In Eq. 8, the preferred value for the base side (230.34 m) of the pyramid in antiquity was used. Remember that this method also incorporates π since that estimate is based on the idea that the height is related to the base as a function of π. This time the measurement closely matches the meridional radius of curvature at the equator and corresponds to what Hancock stated. The difficulty with this approach is that there is considerable variance in the possible values of the Great Pyramid’s size that Hancock simply resolves by fiddling with the base perimeter until a perfect match is claimed. The actual calculation resulted in 39,803 km versus an actual equatorial circumference of 40,075 km).

Hancock must play a back and forth game with numbers until he believes he has found starting points that best fit his desired ending points. Eckhart plays a lot with the base sides, eventually taking an average of two measures (among dozens of choices), and cherry picks his numerator to “show” that 43,200 solves the pyramid to earth comparison to many decimal places.

The actual circumference of the earth, at the equator, is 40,075 km. It can be directly seen that Hancock’s calculation of 39,802.75 does not match. However, since Appendix A provides ranges for the earth’s radii, and since someone might suggest the ancient Egyptians measured the radius at the equator, this analysis will continue by looking at both 6,332.26 km (the implied polar radius) and 6334.80 km (the implied radius at the equator).

At this point it is very helpful to note that the two methods in Eq. 7 and Eq. 8 result in two implied radii that are close (6,332.26 km and 6334.80 km). Being close is naturally expected if the pyramid was built with the idea of a single circle in mind rather than precisely coding the earth’s actual equatorial circumference and the earth’s actual polar radius independently. Also, π was used to calculate the implied radius in Eq. 8, and for Eq. 7 the radius was directly given. But what if the ancient Egyptians did not use π? What if they used a common approximation observed throughout antiquity, such as 22/7? Using 22/7 in Eq. 8 instead of π produces and implied radius 6,332.26 km, an exact match!

An exact match need not be a surprise. That must be the case if the original height of the pyramid equates to the radius of a single circle whose circumference is equal to the base perimeter of the pyramid, 22/7 is used in place of π, and the estimates of the original height and base sides are accurate. (The assumed original measurements are height = 280 cubits and base side = 440 cubits. These round cubit measures are complementary to 22/7).

AXIOM 2: For any pyramid, if the base perimeter divided by the height is equal to 2π, then the following two identities cannot both be correct:

1) The pyramid height times a scalar, k, equals the earth’s polar radius (Circle A).

2) The pyramid base perimeter times a scalar, k, equals the earth’s equatorial circumference (Circle B).

This is because the polar radius and the equatorial circumference each describe two different circles, A and B respectively. Conversely, if both the height and the base perimeter, when multiplied by the same scalar, independently equate to two different dimensions of earth; that is, if the height of a pyramid describes Circle A, and the base perimeter describes Circle B, then the ratio of the base to the height can never be 2π!

Given:

• Circle A ≠ Circle B

• Circle A Radius = Pyramid Height * k

• Circle B Circumference = Pyramid Base * k

then:

• Pyramid Base / Pyramid Height ≠ 2π,

because of the following contradiction:

• Circle B Circumference / Circle A Radius ≠ 2π

It is not clear if Hancock understands these geometric requirements, but he has stated the opposite; that the Great Pyramid does describe π, and that it equates to two independent dimensions of the earth (Hancock & Bauval 1997). Even as he does, he naturally discovers errors that he simply accepts as being within a reasonable range, though his hypothesis fundamentally violates the very geometry that he claims the ancient Egyptians were purposefully modelling.

Appendix C summarizes calculations independent of Hancock and based entirely on evidence. Those calculations demonstrate how both the height and base perimeter of the Great Pyramid likely corresponds to a single circle. Whether that single circle represents some aspect of the earth has not yet been definitively shown.

The Axial Precession of the Earth and the Search for how it Relates to a 43,200 Scalar

As the earth spins on its axis, that axis wobbles. The wobble is somewhat uniform and creates a small circle which is called precession. Precession exists for all spinning disks or spheres. For the earth, one full cycle of precession is completed roughly every 25,920 years, though 25,771.5 is the most recent modern estimate. Hancock et al. gravitate towards 25,920 for various reasons so this analysis will continue using Hancock’s published value of 25,920 (Hancock 2011). However, more precise values for precession are also considered in Appendix E. Hancock claims that the scalar of 43,200 also indicates direct knowledge of precession, and that the cycle the ancient Egyptians calculated was specifically 25,920 years. To verify this requires verification that the Great Pyramid was built with a purposeful scalar of 43,200, and that the scalar also purposefully indicates the number 25,920.

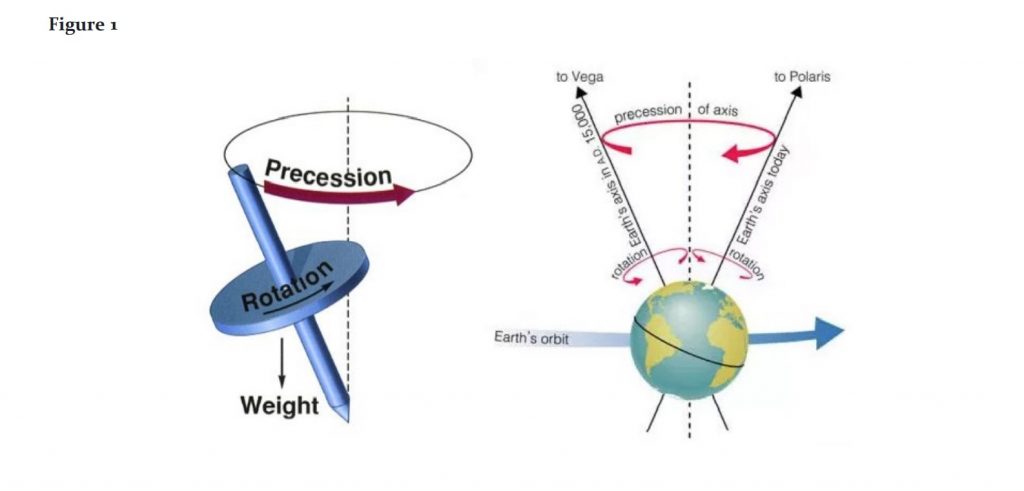
Hancock connects 43,200 to 25,920 primarily because 25,920 divided by 360 gives 72 and 72 is also a factor of 43,200.

Clarification: In the video referenced above, Hancock rounds precession to 26,000. In other videos and publications, he specifies the more precise number of 25,920. This discrepancy in the video is likely conversational rounding. Hancock does point out in the video that the number is the product of 360 * 72. Therefore, it is assumed that Hancock generally prefers the more precise value of 25,920 and focus will be on analyzing that number instead of 26,000. However, as 25,920 is analyzed, all criticisms also apply to 26,000.

Attention is carefully called to any argument where 26,000 might be more beneficial to Hancock’s hypothesis that the Great Pyramid of Giza coded precession. However, a preference for 26,000 over 25,920 was never discovered.

Hancock accurately states that one degree of precession is completed roughly every 72 years. He then associates precession to his chosen scalar by pointing out that 43,200 divided by 600 is also 72. Hancock likes the number 72 and claims that 72 is often observed in ancient civilizations. And so, he emphasizes the number 72, as if seeing 72 twice from two different sources, regardless of how unmeaningful those sources are, is self-evident that something purposeful and special has been revealed. Hancock also points out that 43,200 is the number of minutes in 12 hours. Hancock’s tone in delivering these revelations displays his personal fascination that they must not only be purposeful, but indicative of an advanced and mysterious knowledge. However, the scientific method requires that it is demonstrated that these relationships are not arbitrary, not coincidental, not forced, and that they specifically describe or imply precession using unbiased measures the earth and the Great Pyramid.

For example, 25,920 itself is only somewhat arbitrary. 25,920 is, roughly, the number of years necessary to complete one cycle (circle) of precession. If any ancient culture clearly demonstrated the importance of 25,920 (or 26,000) it could provide evidence for an understanding of precession and beg for additional investigation. So, if it can be shown that a scalar k = 25,920 was indicated by the dimensions of the Great Pyramid, Egyptologists and historians would have long agreed that the ancient Egyptians understood and coded precession with impressive accuracy.

However, Hancock claims the scalar was 43,200 to scale the Great Pyramid to the earth instead of 25,920 to scale it to precession.

Mathematical minded readers will notice that by equating 43,200 to 25,920, Hancock has created an additional degree of freedom with which he can look for more numerical relationships. He now has two numbers to find interesting associations with instead of one. Yet he markets this freedom as another unique and “discovered” truth. Connecting Hancock’s dots for him, it needs to be shown that 43,200 is not arbitrary, or 43,200 is a product of nonarbitrary factors, and that 43,200 or its factors relate directly and profoundly to 25,920.

Hancock suggests the factors he uses are indeed meaningful, though he does not specify exactly how or why. In addition to (1 * 43,200), 43,200 has fortyone other pairs of factors. Hancock especially likes two of those forty-one pairs (600 * 72) and (3,600 * 12). Though 3,600 is notably missing from 25,920. He also like (360 * 72) which are found in 25,920. He highlights these various factors as if it is self-evident that they are purposeful but does not offer any specific evidence how or why they must be special. Many do include the factor of 60, and Hancock favors 60 because of its obvious association to present day time keeping and a 360-degree circle.

It is known that the Sumerians used a base 60 counting system about the same time that the pyramids were built (Ifrah 2000), though solid evidence is lacking that ancient Egyptians adopted a base 60 system for either timekeeping or a circle divided into 6 times 60-degrees. Regardless, clear evidence and intention needs to be shown that the factors 12, 72, 600, and 3,600 purposely connect 43,200 to 25,920 beyond simply explaining that the selected factors are sometimes useful in other applications. For instance, Hancock points out that 25,920 divided by 72 is 360 but even if it is certain that the ancient Egyptians divided a circle into 360 degrees, the question remains why the number 25,920 uniquely indicates the number 43,200 simply because 43,200 also shares factors of 72 and 360. To date, the only thing available that relates precession (25,920) to Hancock’s scalar (43,200) are a handful of common factors which would be common for highly composite numbers and highly factorable numbers.

Hancock provided another relationship; that the number of seconds in 12 hours is 43,200, but this has little use in an evidentiary sense. Not only must it be demonstrated that the ancient Egyptians divided a day into 24 hours of 60 minutes, and 60 seconds, but 43,200 still fails to directly relate to 25,920 years of precession. Hancock fails to provide any connection for these relationships, and an objective inquiry into the facts does not help. For Hancock, he simply rests on pointing out that he appreciates large numbers that possess factors found in present day time keeping. Anyone could continue this game with the other pairs of factors. Frankly, it is surprising that Hancock doesn’t. All the pairs of integer factors of 43,200 and 25,920 are included in Appendix D and certainly people could study them and assign other relationships various factors. Also shown in the appendix is that each factor relationship emphasized by Hancock are shared by many other large numbers in addition to 25,920 and 43,200.

Conclusion

Graham Hancock’s assertion that the Great Pyramid’s dimensions reveal knowledge of earth’s dimensions certainly lacks proof but also fails to hold up to any scrutiny as a viable theory. Each step argued by Hancock; that the Great Pyramid was built to a specific scalar, that the value of the scalar can be definitively demonstrated, that the scalar indicates precession, that the only way ancient Egyptians could estimate precession is to leverage or borrow knowledge from earlier advanced and unrecognized civilizations, are each filled with flaws when taken individually, let alone when strung together to complete his narrative.

Objective evaluations of both the height and base perimeter of the Great Pyramid show that neither are closely comparable to any of earth’s radii when multiplied by his claimed scalar of 43,200. AXIOM 3 states that the deteriorated condition of the pyramid prohibits the calculation of a unique solution equating the Great Pyramid to the earth. Additionally, AXIOM 4 states that highly precise decimal solutions on the order regularly claimed by Hancock et al., cannot exist if the original pyramid dimensions and the scalar were integers. Hancock also claims that his scalar indicates a precise knowledge of precession but offers no support other than pointing out that the scalar and his selected estimate of precession share some identical factors. Although 43,200 and 25,920 share many factors, Hancock selects only a couple that he believes are profoundly important. He offers no evidence for their unique importance other than stating that they relate either to present day timekeeping or a 360-degree circle.

Hancock et al. also like to speak about π being precisely coded into the Great Pyramid. Proof for such claims are also dubious because of the deterioration of the pyramid and the natural characteristic that π exists even when it is not understood. AXIOM 1 states that π would be incidentally incorporated into any pyramid built to match the geometry of a circle. But even more problematic for Hancock is that a pyramid cannot simultaneously contain π and be proportional to two different circles. Hancock claims the Great Pyramid is proportional to both the polar radius of the earth (Circle A), and the equatorial circumference (Circle B). AXIOM 2 states that a comparison to two distinctly different circles is mathematically impossible if the ratio of the dimensions used in the comparisons specifically define π.

While it is acknowledged that the ancient Egyptians may have understood precession, support for such knowledge cannot be found in the basic geometry of the Great Pyramid. Additionally, the general rationale that ancient knowledge of precession is noteworthy because an enormously long observational period is required to estimate it was contradicted in Appendix E. Paragraph

Hancock et al. continue to manufacture mystical relationships and codes with respect to the pyramids. Their intention is part of a broader mission to gather support for a lost Pleistocene civilization that they allege spread advanced knowledge throughout the world before being destroyed by a comet about 12,800 years ago. These nonconformists function to revise and reinterpret archaeological evidence and sites (and sites that are entirely natural) world-wide to narrowly and falsely formulate support for the lost civilization. Their work is rarely scholarly, choosing instead to selectively exploit mainstream archaeology to the extent opportunities exist to distort or repurpose evidence, and reject all archaeological evidence and academic interpretations otherwise. With respect to the pyramids, documenting and debunking each new claim of mystical hidden meaning is never ending, but it is amply clear that their methods consistently rely on selecting input values that confirm desired outcomes, as well as misunderstood mathematical principles.

(To Part 2 – Apppendices)