A Critique of Graham Hancock’s Forced Numerical Relationship between the Great Pyramid of Giza and Earth’s Dimensions – 2: Appendices

(From Part 1)

APPENDIX A – RADII OF THE EARTH

It is impossible to singularly describe the radius of the earth. This is primarily due to the earth being an oblate spheroid instead of a sphere. In an oblate spheroid, every major cross-section (cross-sections that cut though the center of the earth) is an ellipse, of varying sizes, except for the single circle formed by the major cross-section at the earth’s equator. Essentially, the earth is squashed at the poles and bulges at the equator. So, the actual radius at the poles is shorter than the radius at the equator. In addition to this, the varied curvatures at the surface of the earth equate to implied radii that are typically not equal to the actual radii.

Radius of Curvature: Since the earth is squashed at the poles the surface curvature of the earth at the poles complements a sphere that is larger than the actual size of the earth. The radii of curvature are thus the radii that equate to spheres implied by the surface curvatures. As a result, the radii of curvature at the poles is greater than the radii of curvature at the equator. Since the major cross section of the earth at the equator is an actual circle (excepting for topical geography), the East to West curvature exactly matches the cross-sectional circle and the radius of curvature and the actual radius are equal. This is shown in Figure 2 below, where R is the actual radius and N is the radius of curvature in the East/West direction. At 0 degrees, the latitude at the equator, both R and N are equal to 6,378 km.

Figure 2 shows three distinctly different methods for measuring the radii of the earth and how each vary by latitude:

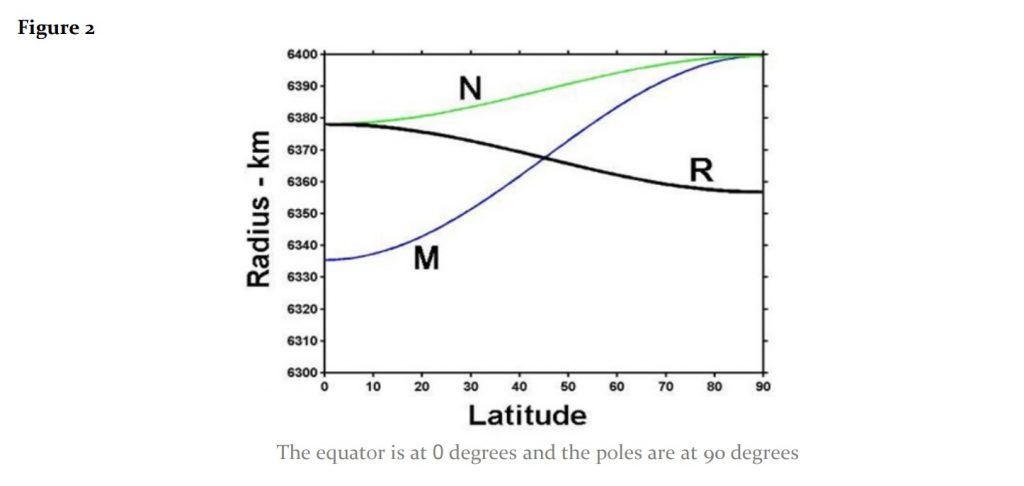
M – The meridional radius of curvature. M describes radii implied by the surface curvature along the meridians. The meridians extend North/South.

N – The prime vertical radius of curvature. N describes radii implied by the surface curvature perpendicular to the North/South curves of M.

R – The actual measured radius from the center of the earth to the surface.

These radii reflect both actual radii (R) and radii of curvature (M and N). The actual radii are somewhat intuitive. They are the actual distances from any point on the surface of the earth to the center of the earth. Since the earth is squashed (from top to bottom) and bulges at the equator, these real distances from the surface of the earth to its center are shortest at the poles and greatest at the equator. At 90 degrees, the actual radius, R, is only about 6,357 km, while at 0 degrees the actual radius is about 6,378 km.

The radius of curvature is the implied radius based on the curvature at any point on the surface. At the equator, because of the lack of squashing seen at the poles, the curvature is tighter and equates to a smaller radius than at the poles. At 0 degrees, the implied radius based on curvature, M, is only 6,335 km, while at the poles (90 degrees), where the earth is squashed flatter and the curvature is wide, a radius of 6,400 km is implied.

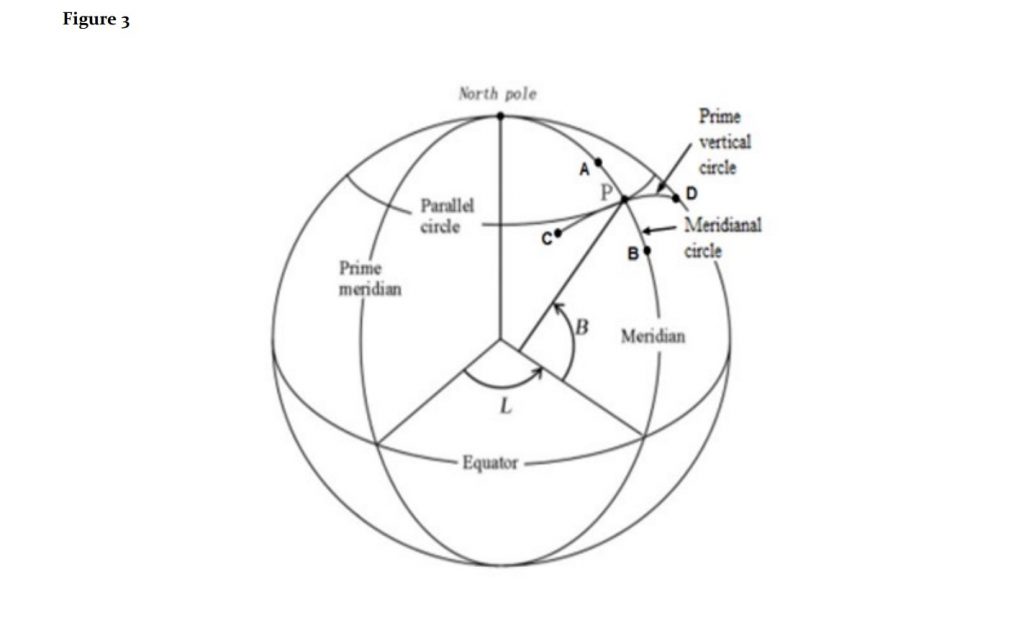
Similarly, curve N represents the change in curvature from the equator to the poles along the prime vertical radius and represents curves perpendicular to M. N is the most difficult cross section to visualize. Prime vertical curves, N, are drawn horizontally from “C” to “D” in Figure 3 below where meridional curves, M, are drawn vertically from “A” to “B”.

APPENDIX B VOLUME OF THE GREAT PYRAMID (Illustration Calculation)

This calculation illustrates how easy it is to equate the Great Pyramid to the earth. Hancock et al. did not perform this calculation in any published work encountered.

Given that a pyramid is built with a perimeter equal to the circumference of a specified circle, and the height of that pyramid is equal that circle’s radius, the following results would follow with respect to volume:

• Eq. 9: Volume of a Sphere: (4/3 * pi * radius cubed) = 4/3 πr³

• Eq. 10: Volume of a Pyramid: (base length * base width * height) / 3 = (lwh)/3 For a pyramid with equal base sides (a square base):

• Eq. 11: Volume of a Pyramid = (base * base * h)/3 = (b² * h)/3

Rewrite the volume of a Pyramid in terms of a sphere. Pyramid Base = (from Eq. 6 above), (2πh)/4 = (πh)/2 substitute the base shown in Eq. 6 into Eq. 11 gives:

• Eq. 12: Volume of a Pyramid = [((πh)/2)² *h]/3 = (π² * h³)/12 Finally, dividing Eq. 9 (volume of a sphere) by Eq. 12 (volume of a pyramid) gives the ratio of a pyramid’s volume to a sphere’s volume:

Eq. 13: Ratio of a Pyramid to a Sphere (in volume) = (4/3 πh³) / (π² * h³)/12 = 16/π

So, to convert the Great Pyramid’s volume to the volume of the earth (if the earth was a perfect sphere), multiple the volume of the pyramid by 16/π and a scalar factor (the scalar is cubed to account for volume). Remember that Hancock claims that the scalar is exactly 43,200.

• Continuing with Eq. 10: Volume of the Great Pyramid of height 146.58 m and a base side of 230.34 m = 230.34² * 146.58 /3 = approximately 2,592,341 cubic meters

• Continuing with Eq. 12: Volume of the Great Pyramid of height 146.58 m = (π² * 146.58³)/12 = 2,590,256 million cubic meters

Starting with the volume of the earth:

• Eq. 14: Volume of the Earth = 1.08321 * 10²¹ cubic meters (exact modern measurement)

• Eq. 15: Volume of the Earth divided by Eq. 13 * 43,200 cubed: 1.08321 * 10²¹ cubic meters / (16/π * 43,200³) = 2,638,100 million cubic meters

Each of these calculations is close given the parameters used. But it is easy to force them all to be exact. If 22/7 is used in Eq. 12 instead of π, 2,592,341 cubic meters is the result. And if the volume of the earth that equates to the radius provided above in Eq. 7 (6,332.26 km) is used, instead of the actual measurement shown in Eq. 14, 2,592,341 cubic meters is again the result.

Algebraically, these equivalent results are already expected and understood for calculations with underlying parameters that are also equal. Of course, instead of pointing out these algebraic identities, each calculation could be performed such that they are all equal and the results presented as another fascinating revelation.

APPENDIX C – INDEPENDENT ESTIMATES BASED ON EVIDENCE

There was no intent in this analysis to discount the knowledge or the ingenuity of the ancient Egyptians or even their possible desire to use the Great Pyramid to describe the size or movements of the earth. This Appendix therefore offers the most likely measurements of the Great Pyramid and how close those measurements relate to the earth based on objective considerations.

Great Pyramid Measurements

The accepted height and base measurements for the Great Pyramid, in antiquity are (Levy 2007):

• Height: 280 cubits

• Base side: 440 cubits

• Perimeter: 1,760 cubits

If these measurements are correct, they immediately reveal that the pyramid was constructed with the geometry of a circle in mind and with the value of π being approximated by the natural number 22/7. Substituting 22/7 for π, and setting the radius to 280 cubits, a circle is produced with a circumference of 1,760 cubits. This is equal to the base perimeter of the Great Pyramid. These measurements seem harmonious with each other, if merely because each are whole integers.

Of course, it is possible that the ancient Egyptians understood π more precisely than 22/7 and that one or more of these preferred measures are incorrect or not integers. For example, if the ancient Egyptians understood π perfectly, and they designed a pyramid with a base perimeter of 1,760 cubits, the resulting height would be 280.11 cubits instead of 280.00 cubits exactly. If the height was selected as 280 cubits exactly, then the implied base perimeter would be 1,759.20 cubits instead of 1,760.00 cubits .

The use of round numbers seems more harmonious and more likely. Also 22/7 is an extremely close approximation for π. In fact, 22/7 is so close that if the ancient Egyptians laid out a circle with a radius of 100 cubits (about 172 feet), the difference between the actual circumference to the calculated circumference using 22/7 is only 0.253 cubits, or 5.2 inches of a circle about 1,079 feet in circumference. Such an error would be very difficult to confirm performing practical experiments and measuring the resulting circumference and radius explicitly.

Scalar Measurement

Rejecting Hancock’s value of k = 43,200 as a given starting point, unbiased calculations of the scalar based on the known size of the earth and the accepted size of the Great Pyramid are now produced.

Note that the complete set of radii, from Appendix A, are in the range of about 6,335 km to 6,400 km. Converting this to cubits is 12,101 cu to 12,225 cu. Using the accepted size of the Great Pyramid, height and perimeter of 280 cu and 1,760 cu, respectively, k is calculated and expressed as a range since the possible radii of the earth is a range.

• Earth’s radii range: (12,101.2, 12,225.4) in cubits

• Earth’s circumference range: (76,064,686, 76,845,371) in cubits

• Range of k implied by the pyramid’s accepted height: (43,219, 43,662)

• Range of k implied by the pyramid’s accepted perimeter: (43,219, 43,662)

As has been demonstrated and discussed previously, it is already clear that the implied range of “k” for both the height and perimeter would be equal since both measurements are compatible with a 22/7 circle.

Starting with a proper range of radii, and the accepted measurements of the Great Pyramid, the scalar 43,200 isn’t even in the range of expected possibilities.

APPENDIX D – FACTORS of 43,200 and 25,920

Listed in this appendix are the pairs of factors for both 43,200 and 25,920. One could play with these at length to find interesting ways to relate them to each other, the Great Pyramid, or some other number associated with the earth or ancient civilizations. The numbers in BOLD highlight matches between 43,200 and 25,920.

43,200 factors: (43,200, 1), (21,200, 2), (14,400, 3), (10,800, 4), (8,640, 5), (7,200, 6), (5,400, 8), (4,800, 9), (4,320, 10), (3,600, 12), (2,880, 15), (2,700, 16), (2,400, 18), (2,160, 20), (1,800, 24), (1,728, 25), (1,600, 27), (1,440, 30), (1,350, 32), (1,200, 36), (1,080, 40), (960, 45), (900, 48), (864, 50), (800, 54), (720, 60), (675, 64), (600, 72), (576, 75), (540, 80), (480, 90), (450, 96), (432, 100), (400, 108), (360, 120), (320, 135), (300, 144), (288, 150), (270, 160), (240, 180), (225, 192), and (216, 200).

25,920 factors: (25,920, 1), (12,960, 2), (8,640, 3), (6,480, 4), (5,184, 5), (4,320, 6), (3,240, 8), (2,880, 9), (2,592, 10), (2,160, 12), (1,728, 15), (1,620, 16), (1,440, 18), (1,296, 20), (1,080, 24), (1,037, 25), (960, 27), (864, 30), (810, 32), (720, 36), (648, 40), (576, 45), (540, 48), (518, 50), (480, 54), (432, 60), (405, 64), (360, 72), (346, 75), (324, 80), (320, 81), (288, 90), (270, 96), (240, 108), (216, 120), (192, 135), (180, 144), and (162, 160).

Someone might consider that the sheer number of matching factors connotes a meaningful relationship. While a meaningful relationship between 25,920 and 43,200 can never be absolutely disproven, it is certainly possible to show that meaning does not exist simply because numerous factors are shared – or even factors important to Hancock are shared. To demonstrate this, many unrelated numbers are selected below to highlighted how easily one number might share factors with another.

Essentially, any large number will work well so long as it includes factors for most of the integers from 1 through 10 (noting that the integers 4, 6, 8, and 9 can be further factored), though 7 is notably absent from both 43,200 and 25,920. Finding such numbers is relatively easy by simply grabbing a handful of integers between 1 and x (where x can be as small as 5) and then multiply them together. Such numbers can be useful in various applications and are similar to highly composite numbers. These numbers can be factored into many base integers and all the integers produced by multiplying combinations of the base integers. So, assessing the relationship of such a number to nature or other numbers will usually provide many options to investigate and shape stories around.

The ancient Egyptians well understood multiplying and factoring, and certainly could have preferred large highly factorable numbers. But if so, such numbers will relate to each other and to other numbers in multiple ways, intentionally or otherwise. Because of this, common factors alone can scarcely provide support for how two numbers can be partnered together.

For comparison, here is a list of many numbers that satisfy the property of sharing factors with 25,920. Each are produced by choosing multiple small integers and multiplying them together.

Each contain the following integers that Hancock particularly likes: 12, 60, 72, and 360.

25,920 = 2⁶ * 3⁴ * 5

43,200 = 2⁶ * 3³ * 5²

23,040 = 2⁹ * 3² * 5

25,200 = 2⁴ * 3² * 5² * 7

28,880 = 2⁷ * 3² * 5²

30,240 = 2⁵ * 3³ * 5 * 7

32,400 = 2⁴ * 3⁴ * 5²

34,560 = 2⁸ * 3³ * 5

38,800 = 2⁵ * 3⁵ * 5

40,320 = 2⁷ * 3² * 5 * 7

45,360 = 2⁴ * 3⁴ * 5 * 7

APPENDIX E – INVESTIGATING THE PRECISION OF PRECESSION (Bonus Illustration using the Mayan Calendar)

The value used by Hancock et al., 25,920, is close to the actual value of precession. Today precession is measured to be about 25,771.5 years. So then, to show that the Great Pyramid does not code precession, it is technically insufficient to simply show that 25,920 is not coded. On one hand, it is fair for Hancock to target 25,920; if the ancient Egyptian did understand precession, perhaps they did estimate it to be 25,920 since a more precise measurement could have been beyond their capabilities. On the other hand, it is curious why Hancock claims that the Great Pyramid was built using hyper-advanced knowledge that humans can’t duplicate today, while touting a value for precession that is not nearly as precise as known today. In any case, the likelihood that the Great Pyramid incorporated precession into its dimensions requires more investigation to fully understand.

To begin with, readers are reminded that nothing near 26,000 was claimed as a Great Pyramid scalar to begin with. Rather, Hancock connects 43,200 to the Great Pyramid, and only connects 25,920 via a few factors with 43,200. It can also be noted that, in Appendix C, the actual scalar was calculated in the range (43,219, 43,662), rejecting Hancock et al. claims that the scalar is precisely 43,200 years. In this analysis estimates are usually expressed as a range, since the earth is not a perfect sphere and has a range of radii.

Hancock suggests the scalar is 43,200. His inspiration and confidence is derived from the simple observation that various factors are shared by both 43,200 and 25,920. Appendix D lists the 42 sets of factors that the 43,200 can be factored into. The supposition that meaning between 25,920 and 43,200 is present simply because some of their factors are similar can’t be entirely discounted though strong skepticism persists when noting that many other ignored factors exist between the two numbers, and the factors that Hancock selected are regularly seen in other numbers. It is also fair to restrict considerations to integers, as Hancock tends to do. Integers tend to be harmonious with nature and easily conveyable interpretations of the observed world, though it is not strictly necessary. If calculations were expanded to the set of all real numbers, then there would be infinitely more flexibility to associate one calculation or observation with another.

However, if consideration is granted that the Great Pyramid coded precession or earth’s dimensions to decimal accuracy (perhaps ever more accurately than 25,920), then it must be conceded that the Great Pyramid was not built to round integer dimensions in the first place (280 cubits height, and 440 cubits base side are the accepted measures) unless the radii of the earth and precession are both coincidentally measured as perfect round integers in cubits. Put another way, if the ancient Egyptians precisely calculated precession or earth’s dimension to decimal accuracy then they would be forced to build a pyramid that couldn’t be expressed with round integers excepting for the infinitesimally small chance that the earth’s dimensions are exact integers when measured in cubits, or by choosing a scalar that is not an exact integer.

That might sound acceptable in principal, but the problem for Hancock et al. is that if the pyramid was not exactly 280 cubits in height and 440 cubits in length for a base side, if it was instead some decimal measure within the range of reasonable possibilities, it could never be known what the original dimensions were because of the deterioration that has taken place.

AXIOM 3: A single unique solution equating the Great Pyramid to the dimensions of the earth does not exist because the deteriorated state of the Great Pyramid does not uniquely indicate uniquely provable dimensions.

Likewise, if the scalar is not a nice integer that can be factored into many other integers, then nothing in Hancock’s hypothesis makes any sense at all. Hancock et al. must live by the integer or die by the integer. This contradiction is at odds with Hancock et al. regularly reporting measures of the pyramid and the earth to many decimal places of precision.

AXIOM 4: A high precision solution equating the Great Pyramid to the earth does not exist if they pyramid was built to integer dimensions and multiplied by an integer scalar.

One either assumes the Great Pyramid was built to harmonious integer measures and proceeds with a search for harmonious integer relationships, or one must immediately give up any hope of demonstrating a singularly profound and hidden relationship given the ambiguity in determining an unknown decimal measure contained in the pyramids original size.

Hancock et al. seem to prefer integer relationships in their initial introductions, but then contradict AXIOM’s 3 and 4 as they find ways to force results to high decimal place accuracy. In this way they can express their mystical arguments that the ancient Egyptians coded knowledge of precession (in addition to various earth’s radii), in a way that resonates with others. If they attempted to show that the scalar is, for example, 43,413.78 (or any other value within the range given in Appendix C), it would be very difficult to excite the layperson about how 43,413.78 relates to 25,920 or the precise measurement of 25,771.5. But then deeper into their presentations they force certain results and report that various obscure calculations matched to many decimal places of accuracy.

Why is a careful precession estimate considered so advanced or mystical inthe first place?

Here is more about the Precession of the Equinoxes, as explained by Graham Hancock (Hancock 2017). 

Hancock et al. gravitate towards things like precession because estimating precession is indicative of a reasonably advanced civilization. This is because a reasonably long period of careful measurements is required to first observe precession, and then to calculate its cycle with some precision. Associating the knowledge of precession with advanced astronomical observation and record keeping techniques is not disputed. Indeed, it takes roughly 72 years for the earth to complete one degree (of 360) of precession. It seems reasonable that it might take 50-100 years for any civilization to generally notice precession and then begin to calculate it. However, the enormously long time that most pseudoscientists claim is required to explicitly calculate long period phenomena is disputed.

The observational requirements to estimate long period phenomena (in the absence of advanced and modern scientific equipment), is a major cause for pseudoarchaeologists to gravitate toward beliefs in older hyper-advanced civilizations. This is a fundamental flaw in their logic because refining estimates for long period phenomena can be accomplished in a fraction of the time the phenomenon completes one cycle. It is not necessary to observe the phenomenon start to finish to calculate its duration with some accuracy, as the pseudoscientists’ arguments tend to require.

Illustration – The Length of the Mayan Year

To first illustrate this point, consider the length of the Mayan year. The exact length of an earth year is 365.24219 days, or 365 days, 5 hours, 48 minutes, and 45 seconds (“Tropical Year.” 2019). This is very close to the length of the Mayan year of 365.24204 days. To refine the length of a year to decimal accuracy, pseudoarchaeologists like to claim that centuries of observation are required. They claim that it would naturally take four years to observe that a year is roughly 365.25 days long.

This rationale progresses as follows: Begin building a calendar and count the days in a year. Only after four years will ancient astronomers be capable of saying that their calendar, relative to the observation of the stars, is off by about one day. Following this linear observation method, the ancient astronomers update their calendar from a year is equal to 365 days, to a year is equal to 365.25 days. (they observed 1,461 days passing until the sun rose or set over the same location, instead of 1,460 days). Continuing in this fashion, they would need another 100 years to notice that they are again off by day. This time they can refine the length of a year from 365.25 days to 365.24 days by dividing 36,524 days by 100 full periods of the sun rising or setting over the same spot (Razzeto 2009).

This method is certainly reliable and might be generally necessary for anyone unable to interpolate between days or years, thereby making partial period estimates using a secondary timekeeping source or intermediate measurements. But, secondary timekeeping methods, intermediate measurements, and even numerical calculation methods are available to better refine an estimate. Even if the ancient astronomers fail to employ an independent and secondary method to accurately measure a portion of a day, at the end 365 days they will still notice that the final day concluded about 1/2, or 1/3rd, or 1/4th a day too soon in comparison to the movement of stars .

Such an observation could prompt the development of methods to suppose when the sun once again sets or rises “on time” without waiting 1,461 days to explicitly see it.

Based on the Mayan calendar it is believed that the Mayan civilization calculated the length of a year as 365.24204 days (Douma 2008). However, other sources convolute the matter and cite a much more accurate measurement of 365.2422 days (Razzeto 2009). Naturally, these seemingly more accurate estimates are more likely to be adopted by the pseudo world because they best fit the fantastic pseudo narrative.

Using the explicit method of relying on full observational periods to adjust the length of a year only after observations are off by one full day implies that the Mayan year of 365.2422 days would require approximately 5,000 consecutive years of observations. For those who accept the explicit method as a reasonable explanation, it does indeed beg the question whether the Mayans received help from an earlier advanced civilization or aliens. Unfortunately, pseudoarchaeologists, who rely upon such limited rationale, proceed immediately to the debate between ancient unknown civilizations versus alien visitation rather than seeking other explanations.

But even if the most accurate estimate in the Mayan year is considered, an explicit method of observing for thousands of years is not required. The explicit observation method ignores the potential use of numerical methods such as period over period averaging, plotting, extrapolation and convergence algorithms, etc., for refining estimates and extrapolating final estimates based on partial period or intermediate measurements.

For example, if an ancient civilization’s astronomers could measure a fraction of a day to within 10 minutes (using the stars or some other time keeping method), then after a single year they could calculate the length of a year as 365 days plus 1/4th of a day +/- 10 minutes. That equates to a range estimate of (365.235, 365.249) days, after only one single observational year. The error in this method is the single error attributed to the final portion of a day measured to within +/- 10 minutes.

If daily calculations are performed for 1,000 days, on day 1,000 the total error is still limited to the final error in calculating a fraction of day 1,000 (still assumed to be about 10 minutes error). That error is now distributed over 1,000 days instead of just 365, and the overall year estimate becomes even more refined. After 10 years not only is the error much smaller in proportion to the observation period, but thousands of day-over-day estimates that can be analyzed with other numerical methods (averaged, plotted, trended, etc.)

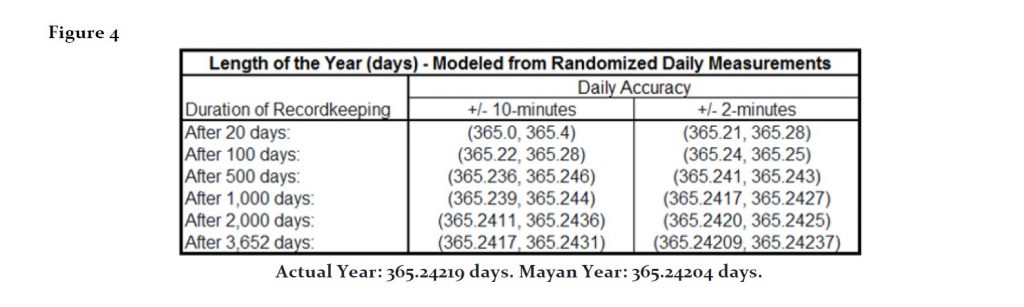
Modeled randomized observations with an average day-over-day error rate of +/- 10 minutes shows that the range can be narrowed to (365.2417, 365.2431) after 3,652 days (about 10 years). The midpoint of this range is 365.24226 and compares well to the actual length of 365.24219 days, and most accurate Mayan estimate of 365.2422 days. Running the model again but with an average day-over-day error rate of +/- 2 minutes, produces a range of (365.24209, 365.24237) and midpoint estimate of 365.24223 days. Remember that it is important in this method to be able to measure a portion of a day using the stars or some other manufactured method or apparatus.

Using a star to mark the onset of an event is not a difficult task. This can be demonstrated by the 18th century English clockmaker John Harrison, winner of the Board of Longitude’s longitude prize. Before winning that prestigious prize, Harrison regularly set his handmade wooden clocks to within 2 seconds by noting a star disappearing behind his neighbor’s chimney (Quill 1963). The ability to note the onset of such an event in time is not difficult. Rather, accurately measuring the amount of time between two known events is where some ingenuity is required. This can be illustrated by using the distance between two points on a line rather than considering time. When two marks are drawn on the earth some distance apart, even if the placement of those two marks are well known, it might be difficult to specify the exact distance between the two. In this way the Mayan’s would need some method for estimating the passing of portions of a single day. Numerous such ideas could be discussed and could have occurred.

The table in Figure 4 demonstrates how the modeled results got tighter by increasing the observation period from 20 days to 10 years. These results also use some simply numerical methods such as averaging and iterated interpolated methods. Such simple numerical methods are at least as old as Archimedes (ca. 200 B.C.) (Burden & Fairs 1989). More complicated methods could also be considered, both observationally and numerical, that could allow for even faster convergence.

The following table displays the modeled results using randomly generated daily measurements. The first column assumes daily measurements within +/- 10 minutes accuracy, and the second column to within +/- 2 minutes. After the random observations the numerical methods are applied to estimate a range around the expected actual length of a year measured in days. The table is an example of how quickly estimates can converge when using a secondary time estimate and some careful application of numerical methods:

Back to Precession

Applying this same type of ingenuity and observational techniques to an ancient civilization’s search for precession could mean that ancients may have enhanced their estimates using fractional observations. Also, as the number of measurements grows, the use of numerical methods makes it possible to estimate a range even more precisely.
For example, if the ancient Egyptians could discern precession through the movement of a rising or setting star after the star moves 1/7th of a degree, they would discern the 1/7th degree movement after approximately 10 years (10.15 years = 1/7th of a degree).

And measuring the location of a star to 1/7th of a degree might not be as difficult as it might initially seem. For example, if ancient astronomers used a large flat area for making astronomical observations and laid out a method for marking locations at one-mile distance from the observation location, then two points separated by approximately 92 feet would represent a single degree. And 1/7th of a degree is represented by approximately +/- 13 feet. It is not too difficult to imagine a group of ancient astronomers siting at the observation location and noting the location of a bright star rising or setting to within 13 feet of its actual location (from one mile). Given that they could complete these observations over the course of many days they could settle on a reasonable estimate. Of course, precession itself would slightly alter those day to day observations but by only 1.3 inches over a 30-day period. Such an error could either be ignored or accounted for using the latest overall estimate of precession.

Imagine that these ancient astronomers begin taking measurements with a precision of 1/7th a degree (or 13 feet from one mile). Suppose that their very first measurement indicated movement of 1/5th of a degree after a duration of time of 15 years (14.21 years is exact). But, of course, their estimate only carries a precision itself of 1/7th degree. Their point estimate would then be 27,000 years (360 degrees divided by 1/5th degree times 15 years). But this early estimate is not very precise since it includes an observational error of +/- 1/7th a degree on an observation of only 1/5th degree. In fact, the measurement of 1/5th degree could have been much larger or smaller given the assumption that the measurement error is 1/7th degree. Regardless, the error component is large in comparison to the observation and the following calculation for the first observation illustrates the range of accuracy.

Observation 1 (15 years):

• Lower bound
= 1/5 degree + 1/7 degree = 12/35 degree
= 360 * 35/12 * 15 years = 15,750 years.
• Upper bound
= 1/5 degree – 1/7 degree = 2/35 degree
= 360 * 35/2 * 15 years = 94,500 years.

(15,750, 94,500) years is quite a wide range after one observation and calculation.

But successive measurements greatly increase the possibility for making more accurate measurements because the successive measurements still have only the single observational error of 1/7th degree and eventually they can be subjected to numerical methods. If a second observation estimates that 2/5th a degree is completed after 27 years (28.41 years is exact), then the error, which is random but still systematically equal to +/- 1/7th degree, is now half the size in comparison to the overall measurement being taken. This is good though our ancient astronomers had to invest twice the time to achieve it.

The point estimate after the second observation at 27 years would then be 24,300 years (360 degrees divided by 2/5th degree times 27 years). But still with a range of +/- 1/7th a degree.

Observation 2 (27 years):

• Lower bound
= 2/5 degree + 1/7 degree = 19/35 degree
= 360 * 35/19 * 27 years = 17,905 years.
• Upper bound
= 2/5 degree – 1/7 degree = 9/35 degree
= 360 * 35/9 * 27 years = 37,800 years.

Note that the range, (17,905, 37,800), has narrowed significantly. Continuing:

Observation 3 (44 years):

• Point estimate = 360 * 5/3 * 44 years = 26,400
• Lower bound
= 3/5 degree + 1/7 degree = 26/35 degree
= 360 * 35/26 * 44 years = 21,323 years.
• Upper bound
= 3/5 degree – 1/7 degree = 16/35 degree
= 360 * 35/16 * 44 years = 34,650 years.

The range, (21,323, 34,650), is even more narrow because the error of +/- 1/7th degree is now getting much smaller in comparison to the observation of 3/5th degree.

Note that other annual observations are possible as well. The ancient astronomers might discern that their star moved 1/2 degree after 34 years (35.51 years is exact). The error in that observation is still roughly +/- 1/7th degree (roughly: because each error of each observation is random though assumed to have an average error of about 1/7th degree). The range given at 34 years would be (19,040, 34,272). Having multiple estimates in this manner allows for even further refinement of the estimate by applying numerical methods to the complete set of observations.

Using mathematics along with careful observation techniques, it is not difficult to imagine ancient astronomers noticing and then making initial (though perhaps rudimentary) estimates of precessions after a few decades of observational recordkeeping.

At any rate, ancient Egyptians certainly wouldn’t require 1,000’s of years of observations to notice that stars were slowing rising and setting in different locations, nor 25,920 years to estimate the time it would take to complete a full cycle. Of course, if they did, they would have observed that precession completed after only 25,771.5 years.

Model Results for Precession

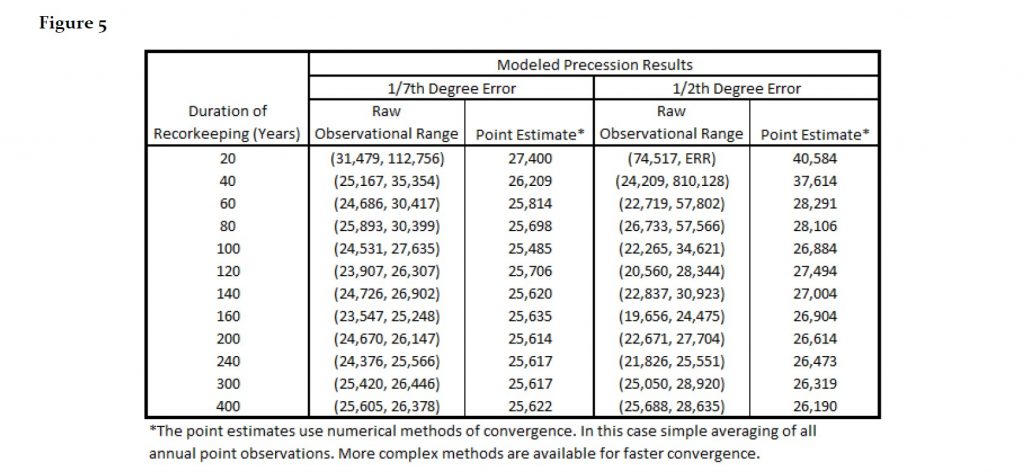
Observational results were modeled assuming observational errors are random and normally distributed with a mean of 1/7th degree. Then simple numerical methods were used to analyze the set of modeled results which produced a point estimate of about 25,485 years after 100 years of observations. Decreasing the precision of the observation from 1/7th a degree to only 1/2 a degree produced a point estimate of 26,884 after 100 years. It should be noted that the modeled results use only a single set of randomized observations – anecdotal to what a group of astronomers might experience when performing real observations. The model results do not display the expected results if the model was run thousands of times. The model also converges to the actual value of 25,771.5 years rather than 25,920 years.

Figure 5 displays the model results. Actual results were recorded annually but the table has been summarized for the years shown.

It is not perfectly clear why an ancient civilization might settle on 25,920, other than acknowledging some of the harmonious aspects that number has with whole integer multiplication. Of course, it might also be that that ancient Egyptians did observe precession but estimated precession to some duration other than 25,920 years.

It is also not clear whether the ancient Egyptians could have measured precession with high precision by the time they designed and constructed the Great Pyramid of Giza, but it is not altogether impossible given the history, accomplishments of earlier dynasties and other earlier civilizations, and the table above which shows that even at 1/2 degree observational accuracy, the value of 25,920 could have been a debatable option within 100 years of observations.

Regardless, to the extent that any ancient civilization borrowed observations and measurements from earlier astronomers, or relied entirely on their own, it can be shown that precession can be estimated in ancient times without indicating the existence of any extremely ancient and hyper-advanced civilizations.

APPENDIX F
WHEREVER π EXISTS, Ø EXISTS

The pages above have already illustrated how a pyramid could include a precise value for π in its geometry entirely by accident. Alternatively, the approximation of 22/7 may have been purposefully used as a proxy for π during the construction of the Great Pyramid. It was also shown that due to the deterioration in the Great Pyramid, if a value for π was purposefully used, and that value was more accurate than 22/7, it would be impossible to determine what the actual value was.

Whether purposeful or accidental, it has been shown that discovering π in the geometry of the Great Pyramid does not indicate a precise knowledge of π as a transcendental number, no matter how accurate one supposes the discovered value of π to be.

Likewise, a close approximation for to Ø would also be discovered in the Great Pyramid as a natural result of either using 22/7 directly or accidentally building in a precise value for π. In other words, wherever π is seen, close approximations for Ø are also present. And as a matter of fact, Ø is even more accurately approximated when 22/7 is used as a proxy for π. This is true because the square of four divided by π and the and the square root of 5/6 π, are both close approximations for Ø.

The mathematical formula for this approximation is simply:

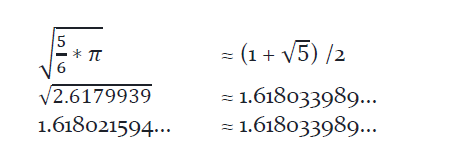
This approximation if extremely close and only differs from the precise value of Ø by 0.0008%!

For Eq. 16a, when using 22/7 for π, the approximation is even closer:

Knowing that whenever π is found Ø must follow, some of the equations previously introduced can be rearranged, some algebra applied, and Ø will be directly found in the Great Pyramid.

Consider Eq. 5:

• Eq. 5: Pyramid perimeter = 4*b = (2πh)

Where “h” is the pyramid’s height “h”, and the base perimeter of that pyramid was set equal to the circumference of a circle with radius “h”.

Rearranging this equation gives:

• Eq. 18: 1/π = h /2b

Multiply both sides by 4 and squaring both sides gives:

• Eq. 19a: (4/π)² = (2h /b)²

The left side of Eq. 19a is nearly equal to Eq. 16a, Ø. So then, it is shown that the square of twice the Great Pyramid’s height divided by the length of a base side is equal to Ø. Ø can be found in other ratios too, but each time it must be a natural occurrence if π can also be found because Eq. 16a is simply and coincidentally a close approximation for Ø. Similar relationships can be contrived to relate Eq. 16b to specific elements of the Great Pyramid.

For instance, Ø is most commonly shown in the Great Pyramid as the ratio of the sum of the surface areas of each face, to the surface area of the base.
Algebraically, this is:

• Eq. 20: 4*F /b² = Ø

Where “F” is the area of a face.

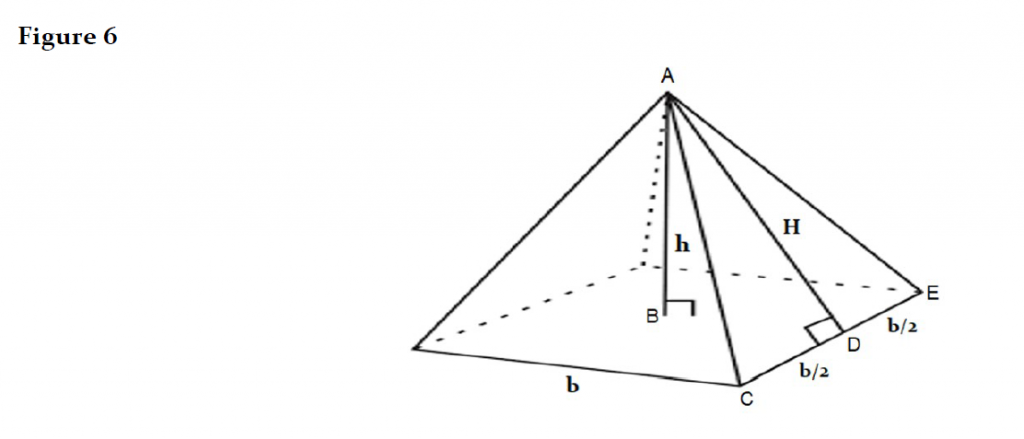
Using the diagram in Figure 6, “F” is calculated and after some algebra and simplification of equations, it can be shown how naturally Eq. 20 must equal or approximate Ø for any pyramid that has embedded π. And π will always be embedded when constructing a pyramid with the geometry of a circle in mind.

• Eq. 21: F = (b*H) /2

Using the Pythagorean formula to solve for “H”:

• Eq. 22:

h² + (b/2)² = H²
H = √[h² + (b/2)²]

Substituting Eq. 22 into Eq. 21 gives:

• Eq. 23: F = {b * √[h² + (b/2)²] }/2

Substituting Eq. 23 into Eq. 20 gives:

• Eq. 24: 4 * [ {b * √[h² + (b/2)²] }/2 ] /b² = Ø

Eq. 24 can be reduced to:

• Eq. 25: 2*√[h² + (b/2)²] /b = Ø
Square both sides and reduce:

• Eq. 26: 4h²/b² + b²/b² = ز (2h/b)² + 1 = ز

From Eq. 18 substitute 1/π = h /2*b

• Eq. 27: (4/π)² + 1 = ز

From Eq. 16a substitute (4/π)² ≈ Ø

• Eq. 28: Ø + 1 = ز

Eq. 28 is a known identity for Ø and one of the reasons it is so special.

So, beginning with Eq. 20 and continuing to Eq 28, it has been shown that for any pyramid, if the height is set equal to the radius of a circle, and the perimeter is set equal to the circumference of that same circle, then approximations for Ø will be found throughout the pyramid if only because Ø is closely approximated by (4/π)² and π is naturally present in such a pyramid. Finding a close approximation of Ø in the geometry of such a pyramid is always purely accidental.

Another identity that is commonly discovered is that the area of each face, triangle (A, C, E), is equal to the square of the height.

In the form of an equation:

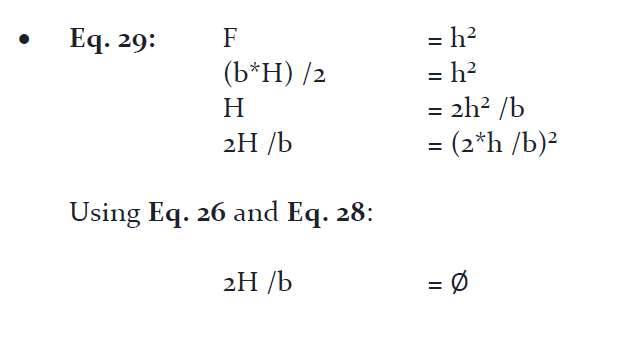
REFERENCES CITED

Burden, Richard L., and John Douglas. Faires
1989 Numerical Analysis. PWS-Kent Publ.

Douma, Michael
2008-01-01 “The Mayan Calendar.” Calendars through the Ages. Institute for Dynamic Educational Advancement. 1 January 2008, http://www.webexhibits.org/calendars/calendar-mayan.html.

“Electronic Distance Measurement Instrument – Types, Functions, Uses.”
2017-09-18 The Constructor, https://theconstructor.org/surveying/electronic-distance-measurement-instrument/6576/. Accessed 30 Oct. 2019.

“Egyptian Pyramid Construction Techniques.”
2019-10-23 Wikipedia, Wikimedia Foundation, https://en.wikipedia.org/wiki/Egyptian_pyramid_construction_techniques.

Hancock, Graham
2017-07-18 “How Do You Think the Pyramids Were Built?” YouTube. John Potter’s.Vision,
https://www.youtube.com/watch?v=E3TQbV6cfQM.

2016-05-23 “Ancient Aliens? Or a Lost Civilization?” The Official Graham Hancock website, Graham Hancock, https://grahamhancock.com/ancient-aliens-or-a-lost-civilization/.

2011 Fingerprints of the Gods. MJF Books.

2017-01-18 “The Precession of the Equinoxes Explained with Graham Hancock.” YouTube, L33T GUY, https://www.youtube.com/watch?v=FunVM44dy_c.

Hancock, Graham, and Robert Bauval
1997 The Message of the Sphinx: a Quest for the Hidden Legacy of Mankind. Toronto: Doubleday Canada.

Keach, Levi
2011 Justifying Belief within the Christian Identity Movement: An Exercise in Memetics. https://www.academia.edu/1481321/Justifying_Belief_within_the_Christian_Identity_Movement_An_Exercise_in_Memetics

Ifrah, Georges
2000 The Universal History of Numbers: from Prehistory to the Invention of the Computer. John Wiley.

Levy, Janey
2017 The Great Pyramid of Giza: Measuring Length, Area, Volume, and Angles. PowerKids Press.

Nightingale, Edward G.
2015-05-20 “The Giza Pyramids and the Precessional Cycle.” The Official Graham Hancock Website, Graham Hancock, https://grahamhancock.com/nightingalee4/. Accessed 30 Oct. 2019.

Quill, H
1963 “John Harrison, Copley Medallist, and the £20 000 Longitude Prize.” Notes and Records of the Royal Society of London, vol. 18, no. 2, pp. 146–160. JSTOR, www.jstor.org/stable/531270.

Razzeto, Thomas
2009 “The Maya Year Is Extremely Accurate.” 2012 Essays by Thomas Razzeto, http://www.infinitelymystical.com/essays/maya-year.html. Accessed 31 Oct 2019.

Schmitz, Eckhart R.
2012-12-30 “THE GREAT PYRAMID OF GIZA: Decoding the Measure of a Monument.” The Official Graham Hancock Website, Graham Hancock, https://grahamhancock.com/schmitze1/. Accessed 30 Oct. 2019.

2012 The Great Pyramid of Giza: Decoding the Measure of a Monument. Roland Publ.

“Tropical Year.”
2019-10-30 Wikipedia, Wikimedia Foundation, https://en.wikipedia.org/wiki/Tropical_year

Yochim, Blair
2015 “Pi and the Great Pyramid.” Vector – The Official Journal of the BC Association of Mathematics Teachers, vol.56, no. 1, pp. 8–15., https://www.bcamt.ca/wp-content/uploads/vector/561-Spring-2015.pdf