Discussions In Egyptology 33, 1995, pp 45-56
Reproduced with permission
In recent articles in this journal, a number of references have been made to the results of my research into the design of the pyramids and other monuments of the Fourth Dynasty; and it has been pointed out that although I do not accept Robert Bauval’s ‘Orion correlation theory’ for the Giza pyramids, [1] I have not as yet offered an alternative explanation for the linking together of these pyramids in a single plan, in terms of the religious ideas which are thought to have motivated the construction of pyramids during the Old Kingdom. Ever since I first demonstrated the existence of the Giza plan in 1979, [2] however, it has been my intention to put forward such an explanation; but I have refrained from doing so because I do not believe that sufficient evidence is yet available from which a secure interpretation of the religious and other objectives of the Fourth-Dynasty pyramid-builders can be determined.
The correct identification of this purpose is to my mind a serious matter, and it is necessary to dissociate the geometrical structure of the site plan – the evidence for which stands by itself and has never been refuted – from speculations concerning the positioning of the Giza pyramids based on a misrepresentation of the Egyptian funerary beliefs. There is, after all, no evidence from the Pyramid Texts or elsewhere to support the idea that different pyramids of the Fourth Dynasty might be equated with different stars of the constellation of Orion; and I find the idea conceptually implausible in view of the fact that successive kings of the Old Kingdom wished to be identified with S3h=Osiris in the afterlife in precisely the same terms from one reign to the next.
Central to this problem is the convenient but vague identification of the word S3h in the Pyramid Texts with the constellation of Orion, when there are good reasons for supposing that the compilers of these texts conceived of S3h not as a constellation, but as a star. This understanding was indeed clearly expressed by Alexander Badawy in his important paper describing the ‘stellar destiny of pharaoh’, in which he referred to Orion as:
| a kind of prince among the other stars’, ‘the most powerful among the stars’, and ‘Orion (probably alpha-Orionis) as the brightest star in the southern sky … [3] |
Although it appears that in later contexts, the name S3h could refer to the constellation of Orion as whole, yet there can be no doubt that just as Sirius stood alone in the sky as the embodiment of Isis, so also only one star in the constellation of Orion could have been supposed to embody the spirit of Osiris, or that of the deceased king in the guise of Osiris. This conclusion is obviously supported in the decan lists of astronomical ceilings, in which the dieties of the different stars are given. In the tombs of Senmut, Pedamenope, and Montemhet, for example, Osiris is associated with the star known as hry rmn S3h, the star ‘under the arm of S3h’; while elsewhere, according to Parker and Neugebauer’s classification, [4] the same star with the presiding deity of Osiris is identified as S3h specifically. Other stars of Orion were referred to in the decan lists as Children-of-Horus and Eye-of-Horus.
As we have seen, Badawy equated the name S3h in the Pyramid Texts with alpha-Orionis, apparently believing that this was the designation of the brightest star in the constellation of Orion when in fact the star in question is named beta-Orionis or Rigel. Since Rigel marks one of the ‘feet’ of Orion, it accords perfectly with the identification of S3h as the ‘Toe-star’, as shown by the translation of the word ‘s3h’; and it also gives meaning to several passages in the Pyramid Texts, including the following as rendered by Badawy: ‘Thou must approach the sky on thy toes as the Toe-star (Orion)’ (PT 723). [5] Substituting Toe-star for S3h in this manner similarly explains the allusion to Seth’s complaint that Osiris had kicked him, ‘when there came into being this his name of Toe-star, long of leg and lengthy of stride’ (PT 959); and likewise the method of ascent of the deceased: ‘I have gone up upon the ladder with my foot on the Toe-star’ (PT 1763). [6] Again, in the Coffin Texts we find: ‘I am the Toe-star who treads his Two Lands, who navigates in front of the stars of the sky on the belly of my mother Nut’ (CT III, 263). [7] This last passage clearly shows which of the two ‘feet’ stars of Orion should be identified as the Toe-star, since when Orion rises in the east, the brilliant Rigel leads the way, and indeed ‘navigates’ because it marks the place on the horizon where Sirius will be seen to rise about 100 minutes later. This indication was of course useful for observations of the heliacal rising of Sothis, alluded to in the naming of Spdt as ‘Year’ in line 965 of the Pyramid Texts.
In passages such as the following: ‘May S3h give me his hand, for Sothis has taken my hand’ (PT 1561), a reference may appear to be made to the anthropomorphic figure of Orion; and yet since this idea cannot possibly have applied to Spdt, there is no reason why it should have applied to S3h either. Consequently, it makes good sense to substitute ‘Toe-star’ for Orion in every occurrence in the Pyramid Texts, and to conclude that the interplay between Isis-Spdt and Osiris-S3h took place in a balanced relationship between two stars – namely Sirius and Rigel, two of the brightest stars in the sky – and not between a star and a constellation. We may infer that the name S3h originally referred to the Toe-star Rigel alone, but was later applied to the constellation of Orion as a whole; yet the Egyptians never lost sight of the fact that only one star in the constellation represented Osiris.
Despite these ‘theological’ objections, I would not have discounted the ‘Orion correlation theory’ if a satisfactory correlation had been shown to exist; but this simply is not the case. I find it surprising that Bauval should have attempted to equate the relative dimensions of the three Giza pyramids with the relative brightnesses of the stars in Orion’s Belt, since when viewed in the night sky, these stars appear almost equally bright, and indeed have similar astronomical magnitudes. Certainly, Mintaka is less bright than the two other stars Alnilam and Alnitak; but when seen in the sky and in photographs, [8] the difference is not very noticeable, and can hardly account for the construction of the Third Pyramid with only one-tenth of the volume of the Great Pyramid. The stars appear naturally as points of light, and not at all as blobs of varying sizes comparable to the bases of the three pyramids, as one might suppose from a time-lapse photograph published by Bauval. [9]
Although the patterning of the stars in Orion’s Belt must be said to resemble the broad disposition of the Giza pyramids, the orientation of the arrangement argues against a deliberate correlation, because firstly the alignment of the Belt stars when referred to the meridian diverged by more than 30º from the corresponding alignment on the ground, for the epoch of around 2500 BC. Bauval has tried to explain this discrepancy by supposing that it was intended to reflect the situation which, due to precession, would have existed in 10450 BC. [10] Still more surprisingly, in order to obtain a correlation with the bend in the line of the Belt stars, Bauval has had to turn Orion upside-down, reversing the positions of the stars from north to south. Thus whereas Mintaka is offset to the north of a line joining Alnitak to Alnilam, the Third Pyramid is offset to the south of a line joining the Great Pyramid to the Second Pyramid. I do not believe that the pyramid-builders, who were acutely conscious of the natural orientations of the star-fields, would have conceived of such a representation; and for this reason alone I do not believe that a correlation was intended between the Giza pyramids and Orion’s Belt.
Three stars do not, in any case, make a constellation, and we must also consider the larger plan which is supposed to encompass the other major pyramids of the Fourth Dynasty. For the reason just cited, and contrary to notion that the stars of Orion were in some way projected on to the landscape beneath them, Bauval has equated the northernmost pyramid at Abu Roash with the star Saiph to the south of Orion’s Belt, while relating the Unfinished Pyramid at Zawiyet el-Aryan to the south of Giza with the northerly star Bellatrix. Now accepting this reversal of the natural ‘geographical’ relationship, and taking the correlation between the Giza pyramids and the Belt stars as fixed, we can determine where the other stars of Orion will fall over Egypt when mapped out on the same scale, using spherical trigonometry to calculate the angular separations of the stars from their celestial coordinates. An accurate comparison can then be made with the distances between the Giza pyramids and the other pyramids of the plan, with reference to a large-scale map such as that published in the Atlas of Ancient Egypt. [11]
Equating the angular distance of 2.78º between Alnitak and Mintaka with the corresponding ground-plan dimension of 936.18 ms between the centres of the Great Pyramid and the Third Pyramid, [12] we thus find that the angular distance of 7.89º from Alnitak to Saiph should correspond to a distance on the ground of 2.66 km. In fact, however, the distance from the Great Pyramid to the Abu Roash Pyramid is about 5 km, or nearly twice the distance required for a correlation. Similarly, the angular distance of 9.18º between Alnitak and Bellatrix gives a distance on the ground of 3.09 km, or less than half the actual distance of about 8 km. The outcome of this analysis, which is easily verified using a computer program such as Skyglobe, is shown in fig. 1. Anything less resembling a correlation would be hard to imagine, and it so happens that neither of the corner stars which were selected by Bauval are the stars closest to their ‘respective’ pyramids. One could, of course, stretch out and rotate the constellation-pattern to obtain a correlation for Bellatrix and Saiph, but in this case the positions of the Belt stars will no longer be represented with any accuracy by the Giza pyramids.
Further objections to the Orion correlation theory will be found in Jaromir Malek’s review of Bauval and Gilbert’s book, The Orion Mystery, together with a clear endorsement of the case for a definable positional relationship between the Giza pyramids. [13] I am grateful to Dr. Malek for his constructive approach to the problem of the Giza site plan, and for his suggestions as to the possible reasons why the three pyramids might have been linked together in this manner. He believes, however, that the relationship could have been built up gradually, and need not have been determined at the outset. In my view, there is good evidence to show that the plan of three pyramids was conceived as an integrated whole in the reign of Khufu; and I intend to discuss this question and the consequences for the significance of the plan in a future article.

The Air-Shafts in the Great Pyramid
Now that Rudolph Gantenbrink has published his findings for the angles of the air-shafts in the Great Pyramid, [14] we must return once again to the question of the supposed astronomical alignments of these shafts. [15] The inclination of the southern shaft from the King’s Chamber, referred to a straight line connecting points near either end and thus excluding possible variations, is now stated to be precisely 45º 0′ 0″, while the slope of the northern shaft is stated to be 32º 36′ 08″. The former is therefore just half the corner-angle of a square; while as Gantenbrink has pointed out, [16] the latter is half the pyramid-profile of 14 rise on 11 base, being close to 7 rise on 11 base or 32º 28′ 16″.
Since the elementary geometrical origin of these angles is clearly indicated, Robert Bauval has sought to explain the design as an example of ‘sacred mathematics’ being used to achieve a religious function; and he has drawn an analogy with the orientation of churches and cathedrals in relation to the eastern horizon. [17] This analogy is invalid, however, because the orientation of a cathedral in no way conflicted with the geometrical concepts which were incorporated within the fabric of the building. Similarly, the precise astronomical orientation of the Great Pyramid with respect to the four cardinal points is entirely independent of the geometry of the structure itself. Given the random positioning of stars in the sky, it must be said that the stellar-alignment theory would have been immeasurably stronger if the angles of the shafts could only be expressed in terms of arbitrary mathematical ratios, for which no very obvious geometrical design could be determined. If the southern shaft was aligned on the diagonal of a square, as Bauval acknowledges, [18] then how much significance can be attached to any star that happened to pass over the shaft-exit at culmination – especially when that star was as irrelevant to the stellar cult as Alnitak in Orion’s Belt?
Interestingly, the inherent conflict between stellar alignments and geometrical requirements was recognised and countered over sixty years ago by Albert Neuburger, who put forward the theory that the southern shafts in the Great Pyramid were aligned towards the brightly shining star Sirius – while also being arranged at right-angles to the sides of the pyramid. According to Neuburger: ‘The four planes of the pyramid were inclined in such a way that the rays of Sirius when culminating fell on the southern plane, hit it exactly at right angles, and passed straight through the ventilating shafts, which also met the plane of the pyramid perpendicularly, into the sepulchral vault, lighting up the sarcophagus of the dead pharaoh.’ [19] Since at the time of Khufu, as Neuburger noted, Sirius culminated with an altitude of about 38º when observed from the latitude of Giza, an alignment would only have been possible with the southern shaft from the Queen’s Chamber; but since this shaft was closed at both ends, it is equally clear that light from Sirius could never have penetrated into the chamber, nor have fallen on the king’s sarcophagus. The conclusion that the shafts intersected the sides of the pyramid exactly at right-angles must, in any case, now be revised in the light of Gantenbrink’s data, as we will see below.
Although I agree with Bauval’s sentiment that mathematics was: [20]
the “architectural language” through which the deeper religious purpose and “function” of the monument can be understood’, and ‘probably considered a “sacred tool” by which the priestly architect could perform his trade,
this trade had also to satisfy mundane practical requirements, in order that the monument could function at all. I have taken the view that the shafts in the Great Pyramid were intended for ventilation and would have served during the building and installation of the pyramid, because the design of the ascending passage-system placed the King’s Chamber much farther from the outside air than in any other pyramid, in a position where hot spent air would inevitably accumulate. If the Queen’s Chamber was less subject to this difficulty – as is supposed to be confirmed by present-day experience – then that only supports my contention that the shafts leading to this chamber were provided as a precautionary measure, and would only have been completed in the event of the failure of the main ventilation-system working through the King’s Chamber, after all the passages and chambers had been roofed over. The ventilation theory is supported by the short route taken from the Queen’s Chamber to the outside of the pyramid, which was chosen in my view not to save time or work, as Bauval has implied, [21] but because it was the best ‘engineering’ solution to the problem, both maximising the air-flow and allowing a convection current to be set up in the sloping shafts, whereby hot air would exit from the southern shaft while drawing cooler air down the northern shaft and across the chamber, as I have previously noted.
For those who assume that the ventilation of a tomb was not a cultic requirement, I must draw attention to those passages in the Book of the Dead and elsewhere, which describe how Thoth was called upon to provide fresh air for Osiris in his tomb. Thus in Spell 182, the ‘Book for the permanence of Osiris, giving breath to the Inert One in the presence of Thoth…’, Thoth proclaims:
I have given the sweet breath of the north wind to Osiris Wennefer,… I give breath to him who is in the secret places.
Again, in Spell 183, we find:
He (Thoth) brings to you sweet air for your nose,… and fair is the north wind which goes forth from Atum to your nostrils, O Lord of the Sacred Land’; and ‘I am Thoth, Lord of Justice,… I have given breath to Wennefer, even the fair breeze of the north wind, as when it came forth from his mother’s womb. I have caused it to enter into the secret cavern in order to revive the heart of the Inert One, Wennefer, the son of Nut…. [22]
The desire to bring the cool north breeze into the tomb in order to revive the corpse of Osiris, therefore, was a concrete requirement of the funerary ritual, and one that may certainly explain the placing of entrance passages on the north side in the pyramids of the Old Kingdom. The theory that these passages were intended to direct the king’s soul towards the circumpolar stars, on the other hand, is purely speculative, and is contradicted by variations in the chosen angles of slope. There seems to be no certain evidence to show that the souls of the deceased needed to be guided in a material sense at all, except for the ka-door which allowed of a magical passage through homogeneous tomb-masonry.
Within the broad framework dictated by the need for a direct route for the ventilating channels in the Great Pyramid from the chambers to the outside, the architect was free to determine the angles according to geometrical principles; and I have previously shown that he was thus able to ensure that each pair of shafts would emerge at exactly the same levels on the north and south sides of the pyramid. [23] In this respect, the measures made available by Gantenbrink have resolved a discrepancy in Petrie’s data, revealing a very interesting geometrical design which explains why these shafts were so carefully constructed. Unfortunately, Petrie did not observe the levels of the outlets directly; but having measured several courses of the core-masonry near the outlets, he tried to place these in the sequence of course-heights obtained by him at the corners of the pyramid. As a result, it now seems clear that he placed the outlet of the southern shaft just one course lower, and the outlet of the northern shaft two courses lower, than was actually the case. [24]
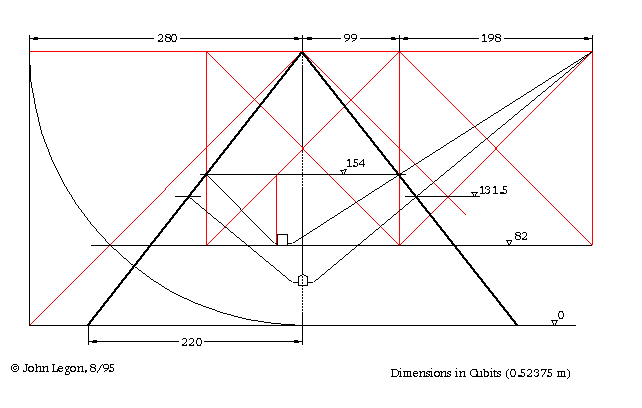
Consequently, it now emerges that the geometry of the air-shafts is entirely a function of the meridian cross-section of the Great Pyramid, and can be developed simultaneously with the geometrical placing of the King’s Chamber which I have previously described. [25] At the same time, the positions of the outlets can be stated in whole numbers of cubits, in perfect harmony with the proportions of the pyramid. The two shafts from the King’s Chamber being now reported to have opened in the casing at the height of 80.63 ms ± 4 cm above the base, [26] they coincided with the level of the 105th course as stated by Petrie ( = 3174.7 to 3176.0 inches above the base, mean 80.65 ms), [27] and defined a level of exactly 2 x 7 x 11 or 154 cubits. The outlet-level was therefore commensurate with the shaft-profile of 7 rise on 11 base, and the casing-profile of 14 rise on 11 base, placing the outlets at a distance of 154 x 11/14 or 121 cubits horizontally inside the base-line of the pyramid. Given the base side-length of 440 cubits, the distance across the Great Pyramid at the level of the outlets was (440 – 2 x 121) or 198 cubits, and thus exactly equalled the height of the pyramid from the floor-level of the King’s Chamber to the apex, of (280 – 82) cubits or 198 cubits. [28]
We can therefore construct the positions of the outlets as shown in fig. 2, by first marking off the height of the pyramid of 280 cubits along the diagonal of a square, to place the King’s Chamber at the level of 280/Ö 2 or 198 cubits below the apex of the pyramid. By forming a square on this height, with the base-side of 198 cubits centred on the central axis of the pyramid, the positions of the outlets on the north and south sides of the pyramid are immediately obtained, and the slope of the southern shaft can be drawn as the 45º diagonal of a square.

The slope of the northern shaft can now be constructed very simply by placing a second square with the side of 198 cubits on the north side of the first. It will be found that the shaft is aligned to the upper north corner of this square, since a line drawn to this corner from the position given for the outlet will have a profile of 7 rise on 11 base, and will therefore define the angle of slope.
It is important to note that the lines of the shafts do not define the offset of the King’s Chamber to the south of the pyramid mid-plane, and that the northern shaft had to begin at the lower end with a longer horizontal and obliquely-sloping section than the southern shaft, before taking up the correct geometrical line. The geometry of the shafts was thus detached from the exact horizontal position of the King’s Chamber, which was fixed by other factors as I have previously shown. [25] Needless to say, if the angles had been fixed by astronomical alignments, then they could have been used directly from the chamber, and the fact that the shafts would then have emerged at differing levels on the north and south sides of the pyramid would have been of no consequence.
Now turning to the shafts leading from the Queen’s Chamber, it so happens that the northern shaft is directed towards the same geometrical ‘focal point’ as the northern shaft from the King’s Chamber, and that the lines of these shafts derive from the same geometrical construction. I have previously noted that if the shafts from the Queen’s Chamber had been completed, they would have opened through the sides of the pyramid at the level of the 90th course, which is 2711.1 inches or 131.48 cubits above the base according to Petrie’s data. [27] This course marks one of the great ‘stages’ in the core-masonry of the pyramid, being noticeably thicker than any of the preceding 44 courses; and it is exactly defined by the centre of the square with the side of (99 + 198) or 297 cubits, which is already given in figure 2 by the distance from the apex of the pyramid to the focal point of the shafts. The level for the outlets is therefore constructed as (280 – 297/2) or 131.5 cubits over the base of the pyramid, giving a profile of 1 rise on (2 – 11/14) base, or 14 rise on 17 base, with a theoretical angle of 39º 28′ 21″.
This angle agrees closely with Gantenbrink’s finding of 39º 36′ 28″ for the southern shaft, given a reported uncertainty in the measurement of 1/5º; while the stated angle of 39º 7′ 28″ for the northern shaft is said to be uncertain within 2º at present, since only a short fractured section at the lower end has been measured. [29] In view, however, of the axial position of the Queen’s Chamber, the near certainty that the two shafts were intended to emerge at the same course-level of the pyramid, and the fact that the horizontal sections at the lower ends are the same length, it can hardly be doubted that the northern shaft was constructed with the same angle of slope as the southern shaft.
While the King’s Chamber is placed at the exact level in the Great Pyramid at which the diagonals of the horizontal cross-section measure 440 cubits, and equal the sides of base, the level of 131.5 cubits for the outlets of the shafts from the Queen’s Chamber is that at which the diagonals of the cross-section measure exactly 330 cubits or 3/4 of the sides of base. Again, at the level of 154 cubits now obtained for the outlets of the shafts from the King’s Chamber, the diagonals measure just 280 cubits, and equal the height of the Great Pyramid. It should be more obvious than ever, therefore, that the design of these shafts was determined by considerations of geometry, symmetry, and the desire for a coherent dimensional design, and can have had nothing to do with the conjectured astronomical alignments.
[1] R.G. Bauval, DE 13 (1989), 7-18; R.G. Bauval and A. Gilbert, The Orion Mystery (London, 1994), passim.
[2] J.A.R. Legon, ‘The Plan of the Giza Pyramids’, Archaeological Reports of the Archaeology Society of Staten Island, Vol. 10 No. 1. (1979); DE 10 (1988), 33-40; GM 116 (1990) 65-72, 71; GM 124 (1991), 69-78.
[3] A. Badaway, MIO Band X, Heft 2/3 (1964), 189-206; 199-200.
[4] R.A. Parker and O. Neugebauer, Egyptian Astronomical Texts, Vol. III (London, 1969), 112-5.
[5] Badawy, op.cit. 201.
[6] Adapted from the translation by R.O. Faulkner, The Ancient Egyptian Pyramid Texts (London, 1969).
[7] Adapted from R.O. Faulkner, The Ancient Egyptian Coffin Texts Vol I. (London, 1973), 180.
[8] For example, see the photographs in P. Moore, Philip’s Atlas of the Universe (London, 1994), 152, 249.
[9] Bauval, op.cit. (DE 13) Pl. 2.
[10] Bauval and Gilbert, op.cit, 193.
[11] J. Baines and J. Malek, Atlas of Ancient Egypt (Oxford, 1980), 135.
[12]W.M.F. Petrie, The Pyramids and Temples of Gizeh (London, 1883), 125.
[13]J. Malek, DE 30 (1994), 101-114; 109.
[14] R. Gantenbrink in R. Stadelmann, MDAIK 50 (1994), 285-294.
[15] See J.A.R. Legon, DE 27 (1993), 35-44; DE 28 (1994), 29-34.
[16] In conversation with the present writer.
[17] R.G. Bauval, DE 31 (1995), 5-13, 6.
[18] Ibid., Fig. 3. Most of the elements in this diagram, albeit deriving very largely from the results of my own research, are irrelevant for the shaft-geometry. The derived northern shaft-angle is incorrect.
[19] A. Neuburger, The Technical Arts and Sciences of the Ancients (London, 1930, reprinted 1969), 343.
[20] Bauval, op.cit. (DE 31), 5, 7.
[21] R.G. Bauval, DE 29 (1994), 23-8.
[22] Adapted from R.O. Faulkner’s translation, The Ancient Egyptian Book of the Dead (London, 1985), 181,184. Cf. CT I,202; II,391; VII,247.
[23] Legon, op.cit. (DE 27), 40.
[24]Petrie, op.cit., 53.
[25] J.A.R. Legon, DE 12 (1988), 41-48, 43.
[26] I am grateful to Robert Bauval for supplying me with this data.
[27] Petrie, op.cit., Pl. VIII.
[28] Despite having noticed this result, R.J. Cook takes the width across the pyramid to be 200 cubits, and consequently fails to perceive the elegant geometry of the shafts. See DE 29 (1994), 29-36; n.9.
[29] Gantenbrink, op.cit., 293.
The Giza Pyramids by John Legon